All for the want of a nail.
"Inevitably, underlying instabilities begin to appear" - Ian Malcolm
So far, I’ve written about:
What “adding value” might mean;
the fundamental building blocks of processes and;
the concept of feedback and how this affects a system.
In this post we’ll introduce the idea of “chaos” or more specifically “chaos theory”.
In the footnote of the previous post, I posed the question, “What does chaos have to do with accounting?” Well, if you’ve been suffering restless nights searching for an answer to that - then you are in the right place!
To the average person, the broad concept of chaos brings to mind the idea of total randomness… here however… we’re talking about a specific brand of chaos.
“Chaos” in systems terms is not random - although it often looks very much like it!
So what exactly is “chaos” then?
In the early 1960s - Mathematician-by-day/Meteorologist-by-night named Edward Lorenz made a discovery that led to the modern field of chaos theory and forever changed how we think about dynamic systems.
In 1961, he constructed a mathematical simulation of the weather using a set of equations that represented changes in temperature, air pressure, wind direction, velocity, and the like. He kept this simulation process continuously running on a computer, iteratively generating a day's worth of virtual weather every minute or so. This process was very successful at producing data that resembled the weather patterns occurring in nature.
However, one day, he wanted to examine a particular sequence at greater length, but in the interests of time, he took a shortcut. Instead of starting a whole new run from scratch, he started midway through, manually typing the numbers output from the earlier run directly as input to continue the sequence from where it left off.
He then went for a cup of coffee and returned an hour or so later to find an unexpected result. Instead of exactly duplicating the earlier run, the new printout showed the virtual weather diverging so rapidly from the previous pattern that, within just a few virtual “monthly" iterations, any similarity between the two had pretty much disappeared.
Lorenz originally thought his computer was faulty, but upon closer inspection, he found this not to be the case. So how did this happen? He ultimately realised that the source of the difference turned out to be a rounding error in the last few digits of one of the input numbers. He had entered 0.506 as a starting input to the new run from the output of the previous run which had been rounded from its original underlying value of 0.506127.
So what changed here?
At the time, most scientists would’ve assumed that such a tiny difference would have dissipated, having no consequence as the calculations were repeated. But it didn’t. The difference amplified through each iteration via our old friend… the positive feedback loop. This phenomenon is known as Sensitivity to Initial Conditions. It’s also sometimes referred to as the “butterfly effect” illustrating the idea that the tiniest of changes - a butterfly flapping its wings - can trigger a series of events that ultimately lead to a tornado.
Before the formal development of chaos theory, most scientific models were linear because these are mathematically simpler. (*Note for us nerds. Yes... Yes… I know…non-linearities were present in some fields, such as fluid dynamics. However, their complexity often meant that scientists used linear approximations as these could still be useful and didn't involve all that complicated stuff with butterflies. Nerd note over.)
Nonetheless, a full appreciation of Lorenz’s experiment and its implications only really happened with the advent of more advanced computers that could handle the many iterative calculations required to study these systems in detail.
The main takeaway from all this is that because there will always be some level of inaccuracy in our measurement we will never be able to accurately predict chaotic systems (such as the weather) beyond a short period. Regardless of how sophisticated our models or how powerful our computers become, any error will grow until our forecast becomes meaningless.
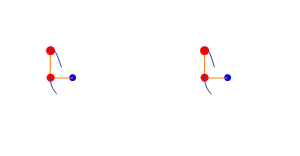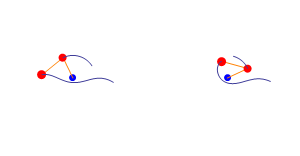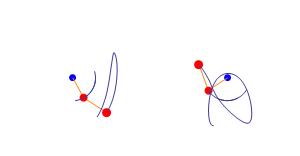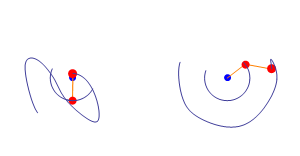
The simplest example of this is what it's known a the “three-body problem” in physics. It's illustrated by a simple double pendulum swinging and just how unpredictable this is. Below, you can see two identical setups starting from (almost*) the same point. (*and when I say “almost” the difference can be at an atomic level.)
Both pendulums (pendula?), maintain similar trajectories initially, but then reach a “tipping point” where they rapidly diverge. These tipping points are an important part of chaos-theory and often appear very suddenly (although they’ve likely built up over a period of time. They’re also irreversible. Think of cliffs suddenly collapsing in to the sea following hundreds of years of erosion. Millenia of stability… then SPLOSH!
OK. This all makes sense, but what does all this have to do with accounting and ultimately the wider question of generating value?
Chaos and Cashflows
Well, many organisations today use cash flow models in some form (normally spreadsheets) to undertake financial planning.
These use a starting set of initial inputs (often the previous month or year’s closing position), apply assumptions and calculations to iterate or “roll-forward” to the next period - repeating the process for the each following period until the plan is complete.
These “cashflow models” are often used to -
Predict a reasonable sequence of outputs (similar in purpose to weather forecasting), or;
Used directly for target setting (representing target output in some form).
Yet, just as weather predictions can be thrown off by tiny measurement errors or unaccounted variables, this same sensitivity when applied to financial forecasts means that slight deviations in early projections can result in significant discrepancies in later financial outcomes. As in Lorenz’s model of the weather, these measurement errors make long-term business planning inherently uncertain and unpredictable.
Recognising the effect of this uncertainty on weather forecasting has led to the transformation of the field of meteorology, shifting the focus from single-path “roll-forward” models to probabilistic approaches; from ignoring small discrepancies to improving data quality (the accuracy/timeliness of any process inputs), and using ever increasing advanced computing power to better manage the inherent unpredictability within the system.
Yet, whilst this underlying and unavoidable unpredictability has the very same profound effect on organisational systems as it does the weather, industry-standard accounting periods, planning methods and long-range forecasts have remained largely unchanged since the Victorian age of ledgers and quills.
Computers have no doubt made these processes faster. But - whilst these processes have become digital in form - their content has remained largely unchanged.
Much of this has to do with the concept of “path dependency” (summarised as “history matters”). Knowledge encoded as professional standards is passed down through multiple generations of professionals and maintains the status quo… through the mechanism of a negative or “balancing” feedback loop.
If anyone deviates too far from the accounting standards, they are nudged back on course. None of the professionals I know enjoy getting told off by auditors and so they happily conform.
So what?
So what’s the problem? This has worked for at least 100 years. Well, on the face of it, it might appear to work, yet traditional financial forecasting really struggles in a volatile complex environment because it :-
Relies heavily on historical data indicating future outcomes and;
Assumes stable relationships between variables.
And as we know from the Lorenz’s experiments, the double pendulum or if you’ve ever invested in the stock market, neither of these things ever holds true for long.
So if we're saying everything is unpredictable...
Why bother planning at all?
Well, I’m not arguing the case that we shouldn’t be planning, but that we should be planning in a different way. Just as this new thinking transformed weather forecasting, organisations need to adopt ways of planning that are more responsive to change and take account of the volatility of the environment in which those plans are expected to operate.
Rapid changes, unpredictable events, and widely interconnected systems make past data (and methods) less reliable and linear models more often inadequate. Additionally, traditional methods are slow to adapt to new information and often overlook qualitative insights like market sentiment or cultural shifts. To thrive in such an environment, organisations need more flexible approaches.
Next time, we’ll look at how the rigid hierarchical structures organisations have traditionally adopted tend to fail in an increasingly dynamic environment, and how modern organisations can structure themselves to deliver value in an increasingly turbulent world.
Again, thank you for reading, I’d be interested to hear your thoughts, and see you next time! And, to know when I next post, you can subscribe using the button below.
Footnote: Yoda (as usual) has a wise - but slightly ambiguous - answer. We’ll try and pin him down to some specifics in iteration 5.